関数解析
関数解析
関数解析の基本事項、及びいくつかの応用に関して記載したマイノートです。今後も随時追加予定です。
目次 [Contents]
- 概要
- 位相空間
- ハウスドルフ空間
- 線形空間（ベクトル空間）
- 点列の収束と極限
- 距離空間
- ノルム空間
- 内積空間
- バナッハ空間 [Banach space]
- ヒルベルト空間 [Hilbert space]
- ヒルベルト空間と射影定理
- 作用素
- 凸最適化理論への応用
- スペクトル理論への応用
- 機械学習への応用
- 参考文献
■ 概要
線形代数学においては、有限次元のベクトル空間を扱い、そのベクトル空間上の写像（作用素）が、行列によって表現できることを見ていた。
一方、関数解析では、有限次元を無限次元に一般化した上で、無限次元を扱うときに、有限次元とは異なることは何か？を議論していくことになる。
その中で特に重要なのが、以下の議論である。
- コンパクト性の問題
- 分解可能性の問題
- 表現可能性の問題（行列のイメージの延長）
- 表現可能性の問題（行列のイメージの限界）
以下の図は、関数解析で扱う各種空間の関係図である。
■ 線形空間（ベクトル空間）
- （例）
１階の線形微分方程式
において、方程式の解（ベクトル）
のすべてからなる集合 V はベクトル空間であることを示す。
に対して、公理 (1),(2),(7),(8) は自明に成り立つ。
に対して、
とすると、
◎ 張る（生成する）
- （例）実数空間を張る（生成する）
n 次元実数空間を
とし、
とする。
このとき、
の任意の 
は、
と書けるので、これらのベクトル
は、n 次元実数空間 
を張る（生成する）。
◎ 線形独立（一次独立）と線形従属（一次従属）
（例）
ベクトル空間として、３次元実数空間
を考え、この空間内のベクトル
のベクトルの組
が線形従属か線形独立かを調べる。- ベクトルの組 が線形従属か線形独立かを調べるために、
を書き下してみると、
② 式より、
よって、
よって、例えば
ならば c_3=1,c_1=−2 となり、
なので、
このベクトルの組
は、線形従属である。
- ベクトルの組
☆ 線形独立（一次独立）と線形従属（一次従属）の幾何学的イメージ
例えば、以下のような３つのベクトルを考える。
これらの３つのベクトルは、何れも z 軸成分が０なので、上図のように、x-y 平面に存在することになる。
これらのベクトルの組 
に対して、
が成り立つことは、直接代入してみれば分かる。
ここで重要なのは、この 
という結果が、例えば、
とかけ、
３つのベクトルの組 の内、１つが他の２つのベクトルに依存（従属）していることを示しているということである。
即ち、これら３つのベクトルの組は、xyz 空間において、特に xy 平面上で互いに無関係ではありえないことを示している。
次に、以下のような３つのベクトルを考える。
このとき、先の関係式と同じ式は、
z 成分が０でないのは、
のみなので、この式において 
でなくてはならない。
については、
この式は、
のときのみ成り立つ。
このように、
という条件は、３つのベクトルの組 
が、３つのベクトルがそれぞれ独立しており、xyz 空間において互いに無関係である（＝独立している）ことを示している。
◎ 基底ベクトル
空間中のベクトルを考える。
以下のベクトルは、上図のようにそれぞれ 
軸方向の 単位ベクトル [unit vector] となっている。
３次元空間中の任意のベクトルは、この単位ベクトル（基底ベクトルとなる）を用いて、
のように、線形結合の形で表現することが出来る！
この単位ベクトルの組 
は、上図から明らかなように、線形独立である。
つまり、
が成り立つ。
実際に代入してみると、
となり、この式が成立するのは、自明に 
のときのみである。
今、３次元空間を考えているが、他に別のベクトル
を付け加えてみる。
すると、この４つのベクトルの組 
に対し、
が成り立つので、このベクトルの組 は線形独立ではない。
逆に、ベクトルの数を減らしてみると、各々の２つのベクトルの組の線形結合、
例えば、
は、z 成分が０なので、線形独立ではない。
そして、任意の３次元ベクトルを表現できない。
つまり、３次元ベクトル空間の任意のベクトルを表現するには、３つのベクトル 
のどれも欠かせないのである！
このように、３次元空間に対して、これらの３つのベクトルが重要な役割を果たしていることが分かる。
そして、このようなベクトルを 基底ベクトル [basis vector] という。
一般に、n 次元ベクトル空間 
に対し、
この空間内の任意のベクトルが n 個の線形独立なベクトルの組 
の線形結合でかける時、これらのベクトルを n 次元ベクトル空間 に対する 基底 という。
◎ ベクトルの次元
基底ベクトルに関して前項で記述したように、３次元ベクトル全体（ベクトル空間）R3 の基底の数は３であった。そして、このベクトル空間内で基底ベクトルの候補となりうるベクトルを１つ付け加えようとすると、これらベクトルの組は線形独立でなくなり、又、基底ベクトルを減らそうとすると任意の３次元ベクトルを表せなく成る。
つまり、与えられたベクトル空間に対し、組み合わせの異なる基底ベクトルの組を考えることはできるが、基底ベクトルの数は変わることがないのである！
このように定まる 基底の数の事を、そのベクトル空間 V の次元といい dim V で表す。
※ ３次元直交直交系のベクトルは３次元であると直感的に使用しているが、ベクトル空間の明確な公理に基づくと次元の考え方は上記のように考えられる。
（例）２次の多項式とベクトル空間の基底（ベクトル空間の公理に基づいた例）
x に関しての２次の多項式
を考える。
この２次の多項式は、定数項
、x の１次の項、x の２次の項から成り立っている。
ここで、各項をベクトルとみなし、
とすると、
任意のベクトルは、
とかける。
このベクトルの組
の内、１つでも欠けると任意の２次の多項式を表現できない。
又、 は、x に関して次数が異なるので、線形独立でもある。
従って、このベクトルの組 は、この２次の多項式によって張られる（生成される）ベクトル空間の基底ベクトルであり、その次元は dimV=3 である。（例）行列とベクトル空間の基底（ベクトル空間の公理に基づいた例）
２×２の正方行列
を考える。この行列を表現するためには、
の４つのベクトルを用意すればよい。
すると、この行列 A は、
とかける。
このベクトルの組
の内、１つでも欠けると２×２の正方行列を表現できない。
又、 はそれぞれ、要素が１となる場所が異なり、それ以外の要素は０なので、線形独立でもある。
従って、このベクトルの組 は、この２×２の正方行列によって張られる（生成される）ベクトル空間の基底ベクトルであり、その次元は dimV=4 である。
■ 点列の収束と極限
世の中には、有限回の計算で完全な解が求まらないような問題が多く存在する。
このような問題では、厳密解への収束が保証される数列（点列）が利用される。
すべての収束や極限概念の基本は、実数列にあるので、
ここでは、この最も単純な実数列を例に収束や極限の概念を定義している。
（数ある数列や点列のうち、具体的に実数列のみを扱うことで一般性は失われるが、実数列で考えたほうがわかりやすいのと、実数列での収束、極限の概念は他の点列でも当てはまることが多いので、実数列のみを取り扱う。）
実数列 
がある極限値 α に収束することを、
や 
などで表現するが、この意味を曖昧さがないように説明するにはどのようにしたら良いだろうか？
この答えとして、以下に定義する ε−N 論法 による定義がある。
◎ 点列の収束・極限に関しての有用な性質
次に、実数列の収束・極限に関して、いくつかの有用な性質を見てみる。
- （証明）
実数列の定義（
）において、ε=1 としても、ある有限な 
が存在し、
が成り立つので、絶対値の部分を変形すると、
を得る。
一方、
は、有限個の実数なので、
これら
の最小値は、
であり、下に有界である。
逆に、これら の最大値は、
であり、上に有界である。
【メモ】
このコーシー列の判定条件と、ε−N 論法におよる収束の定義の違いは？
◎ 上極限と下極限
ここで、実数列が収束するという条件は、厳しい条件になるが、これより弱い条件として、上極限と下極限という概念が存在する。
これは、収束するかわからないような実数列に対しても、大きな n に対して振る舞いを把握した場合に用いることが出来る。
■ 距離空間
距離を用いると、一般の点列の収束や極限の議論が、実数列のときと同じようにすることが出来る。
ここで、距離空間は、ベクトル空間ではなく集合に対して定義されることに注意。
（後述のノルム空間は、ベクトル空間に対して定義される。）
◎ 距離空間の例
（例）１次元の実数での距離空間
実数全体の集合 R において、任意の点
に対して、
距離を
で定義することにより、この写像 d が距離の３つの条件を満たすので（計算略）、
は距離空間になる。（例）N 次元の実数での距離空間
N 次元実ベクトル空間
において、任意のベクトル 
に対して、
距離を
で定義することにより、この写像 d が距離の３つの条件を満たすので（計算略）、
は距離空間になる。（例）距離空間
実数 p≥1 に対して、条件
（和が有限の値で絶対可積分）を満たすような、
すべての実数列
からなる集合を 
と定義する。
すると、この集合 内の任意の 
に対して、
となり、
距離
が定義出来る。
そして、そこから構成される、 は距離空間となる。（計算略）
◎ 距離空間における収束、極限とコーシー列（基本列）
距離空間における点列 
の収束の概念は、以下のコーシー列（基本列）により定義される。
そして、”点列が実数列であるとき、実数列がコーシー列であることと、この実数列がある実数に収束することは等価である！”（証明略）
逆に、一般の点列に対しては、必ずしもこの関係は成り立たない。（証明略）
因みに、点列がある極限に収束するためには、当然ながら極限の情報が必要となるが、
コーシー列の定義では、この極限の情報を必要としていないので、点列がコーシー列であることを示すのに原理上は極限の情報は必要ないことに注意。
◎ 完備距離空間
先の議論で、距離空間 X におけて点列が収束するとはどういう意味であるかはわかったが、
距離空間 X が与えられたときに、ある点列の極限が、その距離空間に存在するか？という問題の解決方法として、極限の候補にあたりをつけ、都度先の収束・極限の条件を満たすか確認する方法も考えられるが、この方法は不便である。
そのような場合に、実数列の場合のとき（＝実数列がコーシー列なら収束する）と同じように、点列の情報だけで極限の存在性が判別できれば便利である。
そのために以下のような、完備な空間というものを考える。
☆ 完備距離空間の例
（例）完備距離空間ではない例
有理数の実数列
は、距離空間 
内において、
に収束するので、この収束先に一意に決まり（収束先の一意性の性質）、
以外のいかなる実数にも収束しない。
また、この実数列
は、有理数 Q の如何なる点にも収束しない。
ここで、距離空間において、点列がある点に収束するならば、その点列は（コーシー列の基本性質より）コーシー列になるので、
この実数列 は、距離空間 のコーシー列になる。
そして、有理数の距離空間
のコーシー列でもある。
従って、この有理数の距離空間 は、完備”でない”距離空間になる。
（一方、実数の距離空間
は、完備な距離空間である。）-
- コーシー列と完備性の関係（＝任意のコーシー列が収束するなら、その距離空間は完備）より、
からなる点列 
が 
のコーシー列であるとき、
この点列が 内のある点に収束するのか調べれば良い。（収束すれば完備）
点列 はコーシー列であるので、
任意の ε>0 に対して、ある
が存在して、n,m>N ならば、
従って、任意の j に対して、（ j = 1 ~ ∞ の無限和なので、）
ここで、j を固定し、実数列
を定義すると、
上記の関係より、この実数列 は、実数空間 R のコーシー列になっていることが分かる。
そして、実数空間 R は完備であるので、 は収束し、
が成り立つ。 - 次に、
は、点列 
の有力な収束先の候補であるが、
実際に、
となり 
となることを示す。
先の
の関係より、任意の
に対して、n,m>N ならば、
記載中...
- コーシー列と完備性の関係（＝任意のコーシー列が収束するなら、その距離空間は完備）より、
☆ 写像の連続性
関数の連続性や微分可能性を調べる際に、変数がある値に限りなく近づく状況を想定し、対応する関数値 f の振る舞いを調べることになる。
この際に、変数が連続的で離散データのように順番を表すインデックスが存在しないので、「変数がある値に限りなく近づく」ということを、予め明確に定義しておく必要がある。
※ この定義の条件（ 
）は、
距離空間 X,Y の開球 
の言葉を用いると、以下のように表現できる。
- （証明略）
- （証明略）
※ この定義の条件（ 
）は、
距離空間 X,Y の開球 
の言葉を用いると、以下のように表現できる。
☆ コンパクト集合
コンパクト性は、距離空間の部分集合に関する性質である。
【Memo】 コンパクトだと、なぜ嬉しいか？
・コンパクト集合上の連続関数は、最大値と最小値を持つ。（後述の最大値と最小値の定理）
→ これにより、最適化の議論が行える。
・コンパクト集合上の連続関数は、一様連続。
→ これにより、近似の議論が可能となる。
※ 特に、距離空間 X 自身がコンパクト集合であるとき、この距離空間 X をコンパクト空間という。
- （証明略）
※ 先の「距離空間のコンパクト」に関する定理は、一般の距離空間で成り立っていたが、この定理では、距離空間 
に限定することで、３つ目の命題も必要十分条件の関係で成り立つようになる。
- （証明略）
- （証明）
を連続写像 f による S の像 f(S) の開被覆とする。即ち、
が成り立つとする。
このとき、U から適当な有限個の開集合を選ぶことにより、f(S) が被覆できることを示せばよい。
（このとき、f(S) はコンパクト集合）
まず、写像 f を逆写像した 
は、”X の” 開集合となり（証明略）、
の関係が成り立つので、この逆写像による集合族 
は、元の部分集合 S の開被覆になっていることが分かる。
ここで、S は X のコンパクト集合なので、この開被覆からうまく選んだ有限個の開集合
から、
とすることが出来る。
従って、f(S) は、
この 
の関係より、f(S) はコンパクト集合であると言える。
- （証明）
まず、最大値の存在について示す。
先の定理（連続写像によるコンパクト集合の像）より、コンパクトな部分集合 S の像 f(S) は、写像先の集合 R のコンパクト集合になる。
このことと、先の定理（距離空間のコンパクト性と点列コンパクト）より、R は有界集合となる。
従って、ワイエルシュトラスの公理（上に有界な任意の部分集合 A⊂R に対し、上限 
が存在する）より、f(S)∈R（有界集合）に上限 
が存在する。
最大値の存在証明のためには、この上限 
が 
となることを示せばよい。
上限の定義から、任意の x∈S に対し、
が成り立つが、
となる実数列 
をとることが出来る。
この実数列 は、
を満たす。
更に、先の定理（距離空間のコンパクト性と点列コンパクト）は、f(S) が（有界）閉集合であることを保証しているので、
となる 
が存在する。
最小値の存在証明に関しても、同様の方法で示せる。
☆ 縮小写像の不動点定理
集合 X で定義された写像 T:X→X に対して、
z∈X が存在して、T(z)=z（＝写像後も変わらず自分自身に写像される点）となるとき、
この点 z は、写像 T の不動点 [fixed point] であるという。
ここでは、写像 T の不動点全体からなる集合を 
と表記することにする。
この縮小写像を用いれば、繰り返し縮小写像することでどんどん距離が短くなるので、
以下の図のように極限となる不動点が表現できる。
※ この縮小写像の不動点定理は、方程式（微分方程式や積分方程式）の解の一意な存在性を示すのに、よく利用される。
この縮小写像の不動点定理の有用性は、写像が縮小写像の場合に限定されるものではなく、
T:X→X が、必ずしも縮小写像ではないリプシッツ連続な写像であっても、T の累乗が縮小写像になる場合には適用される。
☆ ベールの定理
関数解析の線形理論には、corner stones （礎石、基本理念）と呼ばれる４大定理（一様有界性の定理、開写像定理、閉グラフ定理、ハーン・バナッハの定理）が存在する。
この内、ハーン・バナッハの定理以外の３定理は、いずれも完備性がポイントとなっており、以下のベールの定理から導かれる。
このベールの定理（ベールのカテゴリ定理）は、
「完備な距離空間における部分集合を、その閉包（閉集合）が内点を持つか否かという基準で分類すると、2 種類（第１類集合＜疎な集合の和集合で表せる＞、第２種類集合＜疎な集合の和集合で表せない＞）しかない」
ということを主張している。
- 【参考】極私的関数解析：ベールの範疇定理
☆ 稠密 [dense]、可分性 [separable]
実数は、有限桁の小数でいくらでも精度より近似できる。
このことは、非加算無限集合 R が 「”稠密な”可算部分集合 Q の点列の極限」 をもつことに由来しているとも解釈できる。
同様にして、距離空間が稠密な可算部分集合を持てば、本質的には類似の表現が出来ると考えられる。
■ ノルム空間
ベクトルの長さに相当するいくつかの基本的性質のみ抽出すれば、より抽象的な概念として、より一般的な空間にも、ベクトルの長さに相当する概念を導入することが出来る。
この概念こそが ノルム となる。
そして、ノルム空間の２つのベクトル間の距離は、２つのベクトルの差を表すベクトルのノルムとして定義され、この距離によってノルム空間は距離空間になる。
◎ ノルム、ノルム空間の例
（例）
n 次元の複素ベクトル空間
において、
を定義すれば、ノルムの４つの条件式が成り立つので（計算略）、この
はノルムである。
又、
もノルムの４つの条件式が成り立つので（計算略）、ノルムとなる。このように１つの空間に導入し得るノルムは１つとは限らない。
◎ ノルム空間における収束、極限と Cauchy 列（基本列）
ノルムの定義から、距離が ”自然に” 構築できるので、ノルム空間における点列の収束の概念を構築できる。
◎ ノルム空間における完備性
次に、このように定義した Cauchy 列は、収束列であるかを考える。
実数体 R ではこのことは成り立つ。（＝Cauchy 列は、収束列である。）
従って、コーシー列は、実数体 R の中に極限を持ち、このことが、実数体 R の完備性（＝hole がない）となる。
実数体 R は、コーシー列が収束し極限をもつので、完備であったが、
一般のノルム空間は、必ずしも、コーシー列が収束し完備であるとは限らない。
◎ ノルム空間における写像の連続性
- 【参考】 距離空間における写像の連続性
◎ ノルムの等価性
２種類のノルムに対して、互いに等価であるということを、
「等価なノルムを用いる限り、点列がある点に収束するか否かの結論は不変」という視点で定義する。
（証明）
A) まず、前提準備として以下のようなことを考える。
ベクトル空間 X の基底
を１つ固定すると、任意の 
は、
と表現でき、
が一意に決まり、ノルムとして、以下のようなノルム（ノルムの公理を満たす）が定まる。
B) 次に、ベクトル空間 X に定義可能なノルムを任意に選び、これを関数
で表現することにする。この定理の主張（有限次元空間のノルムはすべて等価）を確認するためには、
２つの正数 
が存在して、
が成り立つことを示せばよい。
i. ベクトル空間 X の基底  で表現される任意の 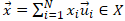 に対して、<br> その  によるノルムは、以下のように変形できる。<br> 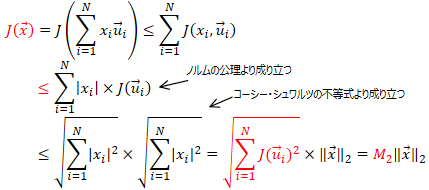<br> 従って、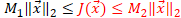 と比較すると、<br> 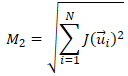<br> が成り立つことが分かる。<br> <br> ii. ノルムに対して成り立つ性質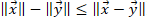（）より、<br> 任意の 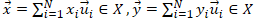 に対して、（先の (B.i) の関係式より）<br> 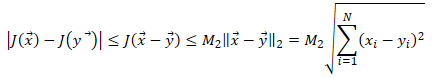<br> となる。<br> 従って、ノルム関数  の写像先を有限にした、関数 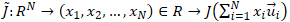 は、<br> ユークリッド空間 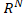 上で定義された連続関数になり、<br> 更に、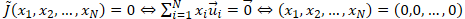 の関係も成り立つ。<br> <br> iii. ここで、<br> 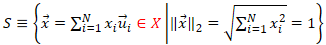<br> 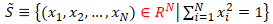<br> を定義すると、<br> この 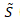 は、 の有限閉集合なので、先のハイネ・ボネルの被覆定理より、コンパクト集合となり、<br> 更に、先の最大値・最小値の定理より、関数 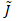 は、 で 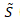 内の最小値を持つことが保証されている。<br> 従って、<br> 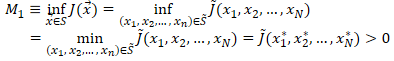<br> の関係が成り立つ。この関係式を変形すると、<br> <br>
まとえると、
及び 
の関係より、
の関係が成り立ち、これはノルムの等価性の条件となるので、
ベクトル空間 X の有限次元空間
の任意のノルムは、等価になるといえる。
◎ ノルム空間における閉部分空間、線形多様体、閉凸集合
ノルム空間は、ベクトル空間でもあるので、部分空間や凸集合といった概念を自然に定義することが出来る。
更に距離空間としての性質も兼ね備えているので、開集合や閉集合といった概念も自然に定義することが出来る。このような概念から構築される、（ノルム空間における）閉凸集合、閉部分空間、線形多様体といった概念は、応用上においても極めて重要な概念となる。
【メモ】
この線形多様体の定義と一般の多様体との関係性は？
→ 線形多様体はアフィン空間のことであり、アフィン空間は最も単純な多様体でもあるため、線形多様体ともいう。
◎ ノルム空間上での写像の微分（ガトー微分とフレッシェ微分）
ここまで、特に無限次元の空間中の点列の収束・極限を考えてきたが、
この収束・極限の概念の延長線上にある微分の概念を、ノルム空間上の写像に対して適用することを考える。
そのためにまず、１変数の実数値関数の微分の定義を簡単に復習する。
- （証明略）図より自明
先に見てきた「１変数の実数値関数の微分」は、「多変数の実数値関数の微分である全微分・方向微分、勾配」 などに一般化出来る。
更に、これらの微分の概念をユークリッド空間からノルム空間に対して一般化したものとして、「ノルム空間上に定義された写像の微分であるガトー微分/
フレッシェ微分」を見ていく。
これらの概念は、最適化問題や変分法に関する議論を行う際に、都合の良い概念になっており、先に見た、「【性質】（１変数の実数値関数の）微分係数の線形近似による特徴づけ」 と基本的な考えは変わらない。
まず、これらの議論に便利な記法（ランダウの記法）から導入する。
☆ ガトー微分
☆ フレッシェ微分
☆ ガトー微分とフレッシェ微分の性質
- （証明略）
- （証明略）
- （証明）
- (a) の証明
フレッシェ微分の定義
を書き換えると、
となるようなある有界線形写像 
が存在し、
となるので、
写像の連続性の条件（写像先での収束 
）を満たすので、
写像 Φ は連続である。
- (b) の証明
点 
における写像 Φ のフレッシェ微分 
を用いると、
任意の
と 
に対して、
ガトー微分の定義
の左辺の lim の中身は、
となり、ガトー微分の条件
が成り立つので、フレッシェ微分 
は、ガトー微分にもなる。
【メモ】
ノルム空間 Y が内積空間である必要性は？
→ 一般化された平均値の定理の写像先の対象空間が内積空間であるため。
- （証明）
D は開集合で、ガトー導関数 Φ′ は連続なので、
任意の ε>0 に対して、十分小さな開球
が存在して、
となる。（下図参照）
又、任意の
に対して、一般化された平均値の定理の関係（計算略）
が適用出来るので、この式を変形すると、
従って、先の
の関係と合わせると、
ガトー微分
は、フレッシェ微分の条件
も満たすことになり、この場合、ガトー微分はフレッシェ微分でもある。
☆ ガトー微分とフレッシェ微分の例
記載中...
■ 内積空間
次に、実数体 R 上のベクトル空間に内積を構築することを考える。
この内積を用いると、ベクトル空間の要素（点）間に直交性などの幾何学的構造を持ち込むことが出来る。
◎ 内積空間におけるベクトルの直交性
◎ 内積空間の性質と内積から誘導されるノルム
内積空間 X の任意の 
に対して、
を定義するとき、この写像 
は、ノルムの公理を満たし、ノルムとなる。
このとこを内積から誘導される（＝自然に道簿行かれる）ノルムというが、このノルムの公理を満たすことを示すために、以下の性質が使用される。
- （証明略）
- （証明略）
- （証明略）
この三平方の定理は、任意の内積空間で成り立つが、n→∞ として級数を無限和、即ち、
とした場合には、完備性の条件を課さなければならない（級数和が収束するため）。
- （証明略）
ここで、内積空間 
において、任意の 
に対して 
がノルムの公理を満たし、ノルムになることを示す。
まず、公理の条件１（ 
）と条件２（ 
）は明らかである。
条件３（ 
）は、
の関係より成り立つことが分かる。
条件４（ 
）は、三角不等式となっており、先の（内積空間における）三角不等式の関係から成り立つ。（尚、この三角不等式自体は、シュワルツの不等式から導かれる。）
従って、ノルムの公理が成り立つので、 はノルムである。
そして、このようなノルムを、内積から誘導されるノルム という。
◎ 内積空間における正規直交系
ここで、内積空間 X が無限次元の場合には、一般に「極大な正規直交系」は、内積空間 X の基底（線形独立なベクトルの極大系）にはならない。
「極大な正規直交系」と「内積空間の基底」が同じ無限次元のベクトルであっても、「極大な正規直交系」の濃度は、「内積空間 X の基底（線形独立なベクトルの極大系）」に比べて小さくなるのが一般的である。
又、この極大な正規直交系は、内積空間が完備であれば（＝ヒルベルト空間においては）、完全正規直交基底となる。
- 【参考】完全直交系 : My_NoteBook/数学/数学フーリエ解析Note.md/直交級数としてのフーリエ級数
☆ グラム・シュミットの直交化法
☆ ベッセルの不等式
【メモ】
フーリエ級数の平均収束から導出されるベッセルの不等式と、この内積空間における正規直交系視点のベッセルの不等式が結びつく。
【参考】２．フーリエ解析入門(２) | Besselの不等式とParsevalの等式
- 【問題2.2】の(1)と(2)、2.3 Besselの不等式とParsevalの等式とで、フーリエ級数の平均収束から導出されるベッセルの不等式と、正規直交系視点のベッセルの不等式が結びつく。
- 【問題2.2】の(1)と(2)、2.3 Besselの不等式とParsevalの等式とで、フーリエ級数の平均収束から導出されるベッセルの不等式と、正規直交系視点のベッセルの不等式が結びつく。
■ バナッハ空間 [Banach space]
先に述べたように、世の中には、有限回の計算で完全な解が求まらないような問題が多く存在する。
このような問題では、厳密解への収束が保証される数列（点列）が利用されることになる。
そういったケースでは、収束先が保証されるように、空間に完備性の構造を課した空間を考えることになる。
- 【参考】ノルム空間の完備性
◎ バナッハ空間の例
（例）バナッハ空間の例（有限次元ベクトル空間）
ベクトル空間
は、任意の種類のノルムのノルム空間で完備であり、
バナッハ空間であることを示す。- 完備であることを示すためには、ベクトル空間 における任意のコーシー列が収束し、極限を持つことを示せばよい。
まずは、簡単のため１次元のベクトル空間 R で考える。
コーシー列を
と記述すると、この点列は有界である（コーシー列の性質）ので、
から構成される点列 
も有界な単調減少点列となり、ある有限な確定値に収束する。
従って、
と書ける。 - 次に、
となることを示す。
コーシー列
に関しては、任意の正数 ε に対して、ある正の正数 
が存在し、
特に、上限 sup で定義されている
で書き換えると、
更に、n→∞ とすると、
を得る。（途中計算略）
一方で、先の不等号 が上限であることを示しており、
が成り立つことがわかる。
更に、n→∞ とすると、
従って、
となるので、結果として、
を得る。
即ち、
のように収束することが示される。 - 次に、先の上限 sup を下限 inf に置き換えて、
から構成される点列 
が有界な単調増加点列となり、ある確定値に収束する。
即ち、コーシー列
の下極限 
となることを利用すると、先の証明と同様にして、
となる。（途中計算略）
最後に、コーシー列の収束先の一意性の性質より、この極限値は一致し、α=β となることがわかる。 - 一般の N 次元ベクトル空間
に対しても、同様の議論が成り立ち、
における任意のコーシー列
が収束し、極限を持つので、
N 次元ベクトル空間 は、完備であり、バナッハ空間となる。
- 完備であることを示すためには、ベクトル空間
）
から誘導される
◎ 有界線形写像全体の集合が作るバナッハ空間と共役空間
有界線形作用素としては様々なもの（行列、微分、積分、フーリエ変換など）が考えられるが、これらの有界線形作用素をかき集めて空間とみなすと、(内積空間やノルム空間を考えたときと同様に）この空間内でのノルム（＝有界線形作用素ノルム）が考えられる。
そして、この有界線形写像全体はベクトル空間となるが、この作用素ノルムによってノルム空間になる。
（【参考】有界線形写像全体の集合が作るノルム空間）
更に、以下の定理で示すように、有界線形写像の写像先がバナッハ空間である場合においては、
この作用素ノルムにより構築されるノルム空間は、完備であり、バナッハ空間にもなる。
- （証明略）証明の方針のみ
B(X,Y) がバナッハ空間であることを示すには、B(X,Y) が完備になることを示せばよい。
そして、完備であることを示すためには、B(X,Y) における任意のコーシー列 
が収束し、極限を持つことを示せばよい。
【メモ】
なぜ、数あるバナッハ空間の中でも、わざわざ有界線形汎関数全体上で共役空間を定義しているのか？
→ （Wikipedia から引用）「一般に双対空間には、代数的双対と連続的双対の二種類が用いられており、代数的双対は任意のベクトル空間に対して定義することができるが、位相線型空間を扱うときは代数的双対よりもその部分線型空間として、連続線型汎関数全体の成す連続的双対空間を考えるのが自然である。」
◎ 一様有界性の定理
先に見たように、関数解析の線形理論には、corner stones （礎石、基本理念）と呼ばれる４大定理（一様有界性の定理、開写像定理、閉グラフ定理、ハーン・バナッハの定理）が存在する。
この内、ハーン・バナッハの定理以外の３定理は、いずれも完備性がポイントとなっており、ベールの定理から導かれる。
ここでは、まず、１つ目の一様有界性の定理を見てみる。
【メモ】
この一様有界性の定理は、バナッハ空間からノルム空間への有界線形関数の各点列での有界性が、そのまま一様有界性（共通の有界づける定数の存在）になることを主張している。
（証明）
- まず、有界線形写像の点列のインデックス n∈N とノルム値の上のしきい値 k∈N に依存する
バナッハ空間 X の部分集合
を導入する。 - バナッハ空間 X からノルム空間 Y への有界線形写像
が、連続写像（＝区間幅から区間幅への写像）であること、
又、
の関係を利用すると、
バナッハ空間 X の部分集合
が閉部分集合であることが導かれる。（途中計算略）
更に、有界線形写像の点列のインデックス n∈N に対しての積集合
も閉集合になることが導びかれる。（途中計算略） - このバナッハ空間 X の部分積集合
が閉集合であることと、
定理の条件（任意の
に対して、ある正数 M>0 が存在）より、
任意の に対して、ある正数 
が存在し、
更に、
に対して 
となるので、
ベールの定理が適用できる条件
が導びかれる。 - ベールの定理より、部分集合
は少なくとも１つの内点を持つので、
少なくとも１つの（内点を与える）正のインデックス
に対して、
ある内点
と r>0 が存在して、
となり、
を得る。
このことから、全ての n∈N について、以下の関係が成り立つ。
更に、作用素ノルムの表現の等価性の関係
から、全ての n に対して、
が成り立つので、
となる。
従って、全ての作用素ノルムを有界づける共通の定数 M が存在するので、バナッハ空間からノルム空間への有界線形写像全体の点列は一様有界である。
- まず、有界線形写像の点列のインデックス n∈N とノルム値の上のしきい値 k∈N に依存する
【参考】
◎ 開写像定理
次に、関数解析の線形理論の４大定理の２つ目の定理として、開写像定理をみていく。
この定理は、有界線形写像により開集合が開集合へ写されるための条件を述べている。
更に、定理の後半部分は、有界線形写像が全単射の場合には、その逆写像も有界線形写像になることを示している。
- （証明略）ベールの定理を利用して証明できる
◎ 閉グラフ定理
次に、関数解析の線形理論の４大定理の２つ目の定理として、閉グラフ定理をみていく。
この定理は、線形写像の有界性を示すための定理になっており、微分方程式の解析や量子力学などで広く応用されている。
【メモ】
ノルム空間 X からノルム空間 Y への連続線型作用素 A のグラフ
が閉集合であることは容易に確認できるが、
その逆（閉集合⇒有界線形写像）を主張するのが閉グラフ定理であり、作用素の連続性の証明に多用される。
- （証明略）ベールの定理を利用して証明できる
◎ バナッハ空間における基底（シャウダー基底）
線形代数におけるベクトル空間の基底は、有限次元で議論されてきた。
一方、関数解析で扱う無限次元のベクトル空間の場合は、線形独立な無限個のベクトルの組の線形結合を扱うので、収束・極限の概念が必要になってくるのが、線形代数での基底の議論と異なる点である。
■ ヒルベルト空間 [Hilbert space]
先に述べたように、世の中には、有限回の計算で完全な解が求まらないような問題が多く存在する。
このような問題では、厳密解への収束が保証される数列（点列）が利用されることになる。
そういったケースでは、収束先が保証されるように、空間に完備性の構造を課した空間を考えることになる。
◎ ヒルベルト空間の例
において、任意の 
に対して、
◎ （旧）３平方の定理や中線定理
要書き換え...
ヒルベルト空間においては、以下のような３平方の定理や中線定理が成り立つ。
この３平方の定理は、任意の内積空間で成り立つが、n → ∞ として級数を無限和、即ち、
とした場合には、完備性の条件を課さなければならない（級数和が収束するため）。
この中線定理が成り立つ時、２つのベクトル 
は、内積の条件を満たすので、内積となる。
更に、
と一致するので、
バナッハ空間がヒルベルト空間であるための必要十分条件は、（バナッハ空間を構築している）ノルムに対し、中線定理が成り立っていることである。
◎ 自己共役作用素（エルミート作用素）と有界性＜閉グラフ定理の応用＞
ここでは、（バナッハ空間の項目で述べた）閉グラフ定理の簡単な応用で導かれる定理を見ていく。
◎ ヒルベルト空間の正規直交系とフーリエ級数
- （証明略）
- 【参考】
◎ ヒルベルト空間における極大な正規直交系
【メモ】
フーリエ級数の平均収束から導出されるパーシバルの等式と、このヒルベルト空間における正規直交系視点のパーシバルの等式が結びつく。
この関係性は、同じく先のフーリエ級数の平均収束から導出されるパーシバルの等式と、内積空間における正規直交系視点のベッセルの不等式が結びつく関係と同じとなっている。
（証明略）
【参考】
◎ 可分なヒルベルト空間における完全正規直交系
- （証明略）
- （証明）
- まず、a ⇒ b の関係（無限次元のヒルベルト空間が可分ならば、このヒルベルト空間は可算個の極大な正規直交系を持つ）を証明する。
- ヒルベルト空間における可分性の定義は、ヒルベルト空間の稠密な部分集合として、可算集合が存在することであるので、
ヒルベルト空間 H の稠密な可算集合（部分集合になる）
が存在する。
この稠密な可算集合 D から、適当にベクトルを選び、ベクトルの組を作ると、
任意の正数 m∈N に対して、これらベクトルの組で張られるベクトル空間
から、線形独立なベクトルの組
を得ることが出来る。
こうして得られた線形独立なベクトルの組 に対して、グラム・シュミットの直交化法を適用すれば、正規直交系 
を構成することが出来る。 - 以下、この正規直交系 U が、極大な正規直交系であることを示すために、
の存在（極大な正規直交系に直交する他のベクトル）を仮定した上で、その矛盾を導く。（極大な正規直交系に対して、直交する他のこの直交系に含まれないベクトルは存在しないため） - まず、極大な正規直交系に直交するならば、稠密な可算集合 にも直交するので、
である。 - 又、稠密な可算集合 D の稠密性（＝ヒルベルト空間に触する）より、
この稠密な部分集合 D 内の点列
の中に、
極大な正規直交系と直交するベクトル
に収束する、即ち、
となるものが存在する。 - しかしながら、これらのことは（
）、
の関係より、矛盾する。
従って、このような は存在せず、正規直交系 U が、極大な正規直交系である。
そして、a ⇒ b の関係（無限次元のヒルベルト空間が可分ならば、このヒルベルト空間は可算個の極大な正規直交系を持つ）が成り立つ。
- ヒルベルト空間における可分性の定義は、ヒルベルト空間の稠密な部分集合として、可算集合が存在することであるので、
- 次に、b ⇒ a の関係（無限次元のヒルベルト空間が可算個の極大な正規直交系をもつならば、このヒルベルト空間は可分）を証明する。
- まず、a ⇒ b の関係（無限次元のヒルベルト空間が可分ならば、このヒルベルト空間は可算個の極大な正規直交系を持つ）を証明する。
- （証明略）
☆ ヒルベルト空間における完全正規直交系の例
- （例）ヒルベルト空間における完全正規直交系の例（L2ノルム）
可算個の点列
を以下のように定義する。
このとき、この点列から構成されるベクトルの組
は、
ヒルベルト空間
（＝ノルムが、
で定義）の正規直交系となる。（計算略）
更に、このヒルベルト空間内の任意のベクトル
に対して、
が成り立つので、パーシバルの等式
が成り立ち、ヒルベルト空間における正規直交系の定義より、
この正規直交系 は、極大な正規直交系であり、完全正規直交系になる。
- （例）ヒルベルト空間における完全正規直交系の例（フーリエ正弦級数展開）
区間 [0:1] の可算個の点列（関数列） を以下のように定義する。
このとき、この点列から構成されるベクトルの組 は、
ヒルベルト空間
（＝ノルムが、 で定義）の正規直交系となる。（計算略）
更に、この正規直交系 は、このヒルベルト空間 の完全正規直交系にもなる。（計算略）
従って、このヒルベルト空間内の任意のベクトル
に対して、
の強収束の関係が成り立つので、
ヒルベルト空間内の任意のベクトル は、以下のような線形結合の形で表現できる。
この内積を積分の形で表現しなおすと、
この式は、フーリエ正弦級数展開に他ならない。
◎ ヒルベルト空間における強収束と弱収束
無限次元空間を扱う関数解析においては、有限次元を扱う線形代数とは異なり、線形独立な無限個のベクトルの組の線形結合を扱うので、空間内の点列の収束性を議論する必要がある。
この際に、強収束の意味での収束を議論することは、扱う対象によっては必ずしも簡単ではないケースも存在する。そこで、この強収束よりも弱い概念である弱収束なるものを導入する。
- 【参考】
■ ヒルベルト空間と射影定理
関数解析の最も広く応用展開されるているものの１つとして、ヒルベルト空間における直交射影定理というものが存在する。この直交射影定理は、ピタゴラスの定理の高次元版であり、ユークリッド空間における幾何学的な直感が、高次元空間でも通用することを示している。
更に、直交射影定理は、最も基本的な最適化原理になっており、
対象となるヒルベルト空間や閉部分集合をうまく設定することにより、多くの応用が可能となる。
これは例えば、フーリエ級数展開が、正規直交系が張る閉部分集合への直交射影の単純な表現を与えていることや、最小２乗推定や一般逆写像やカルマンフィルタの基本的なアイデアも、直交射影定理の応用の１つとなっている。
又、凸射影定理は、直交射影定理を拡張して得られる非線形版であるが、凸最適化問題の基礎となっている。
◎ ヒルベルト空間における凸射影定理と直交射影定理
☆ ヒルベルト空間における凸射影の非拡大性
以下の定理は、凸射影が非拡大写像の一例になっていることを示している。
（証明略）(3) に関しては、図より自明
参考
☆ ヒルベルト空間における直交分解
- （証明略）３次元空間においては、図より自明に成り立つ。
- （証明略）３次元空間においては、図より自明に成り立つ。
☆ ヒルベルト空間の閉部分空間への直交射影の線形性・冪等性・自己共役性
- （証明略）３次元空間においては、図より自明に成り立つ。
- （証明）
- 直交分解の定理より、直交写像 
に関して、任意のベクトル 
は、
のように、一意に分解出来る。
これを利用すると、
- 更に、任意の 
に対して、
となるので、
となり、この定理は成り立つ。
- （証明略）
☆ ヒルベルト空間における和空間への直交写像
- （証明略）３次元空間においては、図より自明に成り立つ。
◎ ヒルベルト空間における線形多様体への直交射影と正規方程式
ヒルベルト空間では、有限次元の部分集合は、”常に”閉集合となる（先のノルム空間における閉部分空間に関する定理より）が、以下の定理で示すように、この有界線形部分空間への直交射影の計算は、次元の数だけ未知数を求める線形連立方程式の問題に帰着される。
（※ このことは、有限次元部分空間への直交射影が、線形代数におけるガウスの消去法を用いて有限回の四則演算で計算できることを意味している。）
従って、有限次元部分空間への直交射影の計算原理を把握しておくことにより、応用上の諸問題（凸最適化問題、最小２乗推定、一般逆写像等）に、直交射影定理をうまく活用することが可能となる。
☆ ヒルベルト空間における直交射影と正規方程式・グラム行列
- （証明）
- まず、「
」⇔「
が正規方程式の解」の関係を示す。
図より、
となるので、直交射影定理より、
部分空間中のベクトル 
に対して、
の関係が成り立つが、この式を変形すると、正規方程式なる。
従って、
となるための必要十分条件が、正規方程式の解の存在となる。
- 次に、「グラム行列 G が正則行列で解が存在する（＝逆行列が存在する）」 ⇔ 「
が一次独立」 の関係を示すために、
その対偶である 「グラム行列 G の行ベクトルが一次従属」 ⇔ 「 が一次従属」の関係を示す。
- 「 が一次従属」 ⇒ 「グラム行列 G の行ベクトルが一次従属」の証明
が一次従属である場合には、
となる非ゼロな係数ベクトル 
が存在する。
このとき、
となるので、グラム行列 G の行ベクトルが一次従属となる。
- 「 が、一次従属」 ⇐ 「グラム行列 G の行ベクトルが一次従属」の証明
グラム行列 G の行ベクトルが一次従属である場合には、
となる非ゼロな係数ベクトル 
が存在する。
このとき、
となるので、
となり、
が、一次従属となる。
☆ ヒルベルト空間における線形多様体への直交写像と最小ノルム点
- （証明略）３次元空間においては、図より自明に成り立つ。
☆ ヒルベルト空間における等式線形制約条件下での線形方程式の解集合と線形多様体への射影
- （証明略）３次元空間においては、図より自明に、線形方程式の解集合が線形多様体になる。
- （証明略）３次元空間においては、図より自明に、V∩M が最小ノルム点になる。
- （証明略）３次元空間においては、図より自明に、
が、線形方程式 
の解となる。
- （証明略）
３次元空間においては、図より自明に、正規方程式 
の解は、
であるので、成り立つ。
■ 作用素
◎ ノルム空間における有界線形作用素
☆ ノルム空間における作用素ノルム
- 【参考】
☆ ノルム空間における有界線形汎関数
- 【参考】汎関数微分
☆ 線形写像の連続性
ノルム空間のような位相構造を持つ空間においては、先に記載したように線形写像の連続性についての概念を構築することが出来た。（参照）
以下の定理で示すように、有限次元の（＝有界な）ノルム空間においては、線形写像は必ず連続である。
（従って、非連続な不連続線形作用素の議論が意味を持つのは、無限次元の空間を扱う場合になる。）
- （証明略）２次元空間においては、図より自明に成り立つ。
☆ 【補足】逆写像の存在性
- （証明略）
- （証明略）
- Wikipedia より引用
☆ 有界線形写像全体が作るノルム空間
有界線形作用素としては様々なもの（行列、微分、積分、フーリエ変換など）が考えられるが、これらの有界線形作用素をかき集めて空間とみなすと、(内積空間やノルム空間を考えたときと同様に）この空間内でのノルム（＝有界線形作用素ノルム）が考えられる。
そして、以下の定理で示すように、有界線形写像全体はベクトル空間となるが、この作用素ノルムによってノルム空間になる。
- （証明略）
☆ 行列の作用素ノルム
２つの有限次元のノルム空間の間で定義される ”任意の” 線形写像は、各々のノルム空間の基底ベクトルで展開（表現）した係数ベクトル間の変換行列によって完全に表現出来る。（＝線形写像の表現行列）
今、議論の対象空間として、
m×n 行列の全てからなる集合 
及び、その要素である m×n の有限次元ベクトル 
を考え、このベクトル空間に定義される代表的なノルムとその性質をみていく。
- （証明略）
行列の作用素ノルムの例
（例）行列の作用素ノルムの例１
n 次元ベクトル空間
から、別の m 次元ベクトル空間 
への線形写像 T:X→Y を、
実行列
を用いて、
のように表現したとする。
このとき、
のノルムを
のように定義した場合に、T の作用素ノルム ‖T‖ は、
と表現できることを示す。
（＝max 条件に対応）を満たす任意の 
に対して、
T の作用素ノルムは、定義より、
と書けるが、この式の
の部分を変形すると、
従って、
の関係が成り立つことがわかる。
ここで、この式の最右辺
の式との等号は、最大値の達成時に成り立つが、
k=p で最大値が達成されるとすると、ノルムが１の単位ベクトル
で式を表現し直すと、
となり、反対方向の不等号も成立するので、
（例）行列の作用素ノルムの例２
先の例と同じ状況下で、ベクトル空間（ノルム空間になる）
のノルムを、
のように定義した場合に、T の作用素ノルム ‖T‖ は、
と表現できることを示す。- 先の例と同様にして、
（＝max 条件に対応）を満たす任意の 
に対して、
T の作用素ノルムは、定義より、
と書けるが、この式の
の部分を変形すると、
従って、
の関係が成り立つことがわかる。
ここで、この式の最右辺
の式との等号は、最大値 max の達成時に成り立つが、
j=p で最大値が達成されるとすると、ノルムが１の単位ベクトル
で式を表現し直すと、
となり、反対方向の不等号も成立するので、
- 先の例と同様にして、
◎ ムーア・ペンローズの一般化逆写像
- （証明）
> 記載中...
☆ ムーア・ペンローズの一般化逆写像の特異値分解表現
記載中...
◎ リースの表現定理
ここでは、ヒルベルト空間上に定義された有界線形汎関数は、内積を使って一意に表現できるというリースの表現定理について見ていく。
まずリースの表現定理を見ていくために、以下のようなことを考える。
先に述べたように、ノルム空間 X から実数空間 R への有界線形写像を、有界線形汎関数というが、このノルム空間 X 上の有界線形汎関数全体からなる集合を 
と書く。
（※ 有界線形写像には、行列、微分、積分など様々なものが考えられるが、これらをかき集めて１つの空間したものが B(X,Y) ）
ここで、 は、写像先の実数空間 R の完備性と有界線形写像全体からなる集合であることにより、この 自身も、作用素ノルム
が定義されたバナッハ空間となる。（有界線形写像の全体集合が作るバナッハ空間の定理より）
更に、ノルム空間の共役空間の定義（＝ノルム空間 
上に定義された有界線形汎関数全体からなるバナッハ空間 B(X,R) が X の共役空間）より、
このバナッハ空間 は、X の共役空間となる。
ここで、リースの表現定理を導入するための前段階として、ノルム空間の有界線形汎関数全体が作る共役空間に関しての以下のような補題を導く。
- （証明略）３次元空間においては、図より自明
- （証明）
の存在性と一意性を示しているが、まず、
の場合
の関係より、
が自明に存在する。
の場合、
となる単位ベクトルが存在し、
は、
を用いて、
の
の項が、この定理の条件 
を満たしていることが分かる。
となる。
の一意性について示す。
に関して、
に対して、
となるので、
を選ぶと、
でなくてはならず、ただ１つのベクトルが存在することになる。
と 
に対して、
となるので、◎ 内積空間上の線形汎関数の表現
リースの表現定理で、ヒルベルト空間とその共役空間の関係性は明らかになったが、次に、ヒルベルト空間ではないノルム空間の共役空間の場合にはどのようになるのかを考える。
より詳細には、簡単のためノルム空間を内積空間に限定した上で、
必ずしも完備ではない内積空間上に定義された有界線形汎関数は、コーシー列と内積を用いて具体的に表現できることを見ていく。
そして、この内積空間の共役空間を構築するプロセスは、先の述べた空間の完備化のプロセスの具体的になっている。
以下、内積空間 X は、
内積として 
が定義されており、
ノルムとして、内積から誘導されたノルム 
が定義されているとする。
任意に選ばれたベクトル 
を用いて、
ノルム空間 X 上の線形汎関数 
を、
のように定義すると、
この線形汎関数 
全体が作る集合は、この内積空間 X の共役空間 
となり、
となる。
又、作用素ノルムは、
となる。
更に、内積空間からその共役空間への写像 
は、
を線形汎関数 
に対応づける１対１の写像（ 
）となっており、
となる。
ここで、ノルム空間 X 上の線形汎関数 
は、
のように定義されているので、
「内積の形で表現可能な有界線形汎関数」となっているが、
逆に、”任意の” 有界線形汎関数は、ノルム空間 X 上の内積で表現できないか？ということを考える。
先のリースの表現定理で述べたように、
ヒルベルト空間 H の場合には、任意の線形汎関数 
に対して、
を満たすベクトル 
が存在していた。
一方、内積空間 X の場合は、内積空間 X 上の全ての有界線形汎関数 
が、
の形で内積表現できるためには、内積空間が完備（＝即ち、ヒルベルト空間）であることが必要になる。（後述）
このことを示すために、まず以下の補題で、必ずしも完備ではない内積空間 X が与えられているときに、内積で表現される有界線形汎関数の全体の集合 
が、内積空間の共役空間 で稠密になり、内積空間 X 上に定義された任意の有界線形汎関数（の作用素ノルム）が、「内積で表現される有界線形汎関数（の作用素ノルム）」によって、いくらでも精度よく近似可能になることを示す。
- （証明略）
- （証明）
- (a) の証明
有界線形汎関数 f の作用素ノルムは、
のように上限 sup の形で書けるので、
となる点列 
が存在する。
- (b) の証明
(a) の 
の関係より、
従って、任意の ε>0 に対して、十分大きな正数 N が存在して、
となるので、先の補題（内積で表現される有界線形汎関数の作用素ノルムの誤差評価）より、
即ち、定理にある
の関係が成り立つことが分かる。
このことは、内積で表現される有界線形汎関数全体の集合 J(X) が稠密であることを示している。
ここで、内積で表現される有界線形汎関数 
の作用素ノルムは、
となるので、このときの場合は、
となるので、点列 
はコーシー列である。
- （証明略）
【メモ】有界線形汎関数の内積表現によるヒルベルト空間の特徴づけ
内積空間 X から実数 R への有界線形汎関数 f:X→R において、この有界線形汎関数全体が作る集合 X^∗=B(X,R) は、この内積空間の共役空間となるが、
「この内積空間 X が完備でない」⇒「内積表現可能でない有界線形汎関数が存在する。」 となるので、内積空間 X 上の全ての有界線形汎関数 ∀f∈X^∗ が、内積の形で表現できるためには、X がヒルベルト空間でなくてはならない。
この要件によりヒルベルト空間を特徴づけることも出来る。
そしてこのことは、リースの表現定理への帰結とみなすこともできる。
◎ ハーン・バナッハの定理
関数解析における４つの corner stoens （一様有界性の定理、開写像定理、閉グラフ定理、ハーン・バナッハの定理）の１つであるハーン・バナッハの定理は、他の３つの定理をとは異なり。空間の完備性を必要としない。
この定理は、一般的には。、ツォルンの補題を用いてノルム空間で議論されるが、ここでは簡単のため、内積空間に限定して議論する。
- （証明）
先の定理（内積空間上の線形汎関数の表現と構成）の (a) より、
有界線形汎関数 
に対して、内積空間の部分空間 M のコーシー列 
が存在し、
のように有界線形汎関数 が表現出来る。
逆に、部分空間 M のコーシー列 は、元の内積空間 X のコーシー列でもあるので、
先の定理（内積空間上の線形汎関数の表現と構成）の (b) より、
によって、有界線形汎関数 
を定義することが出来る。
従って、
となり、この定理の１つ目の式 
は満たされることが分かる。
更に、
の関係より、この定理の２つ目の式（＝作用素ノルムが等しい）も満たされることが分かる。
◎ 有界線形作用素の共役作用素
※ リースの表現定理は、ヒルベルト空間に対しての定理なので、厳密には、この内積空間上での共役作用素の定義に対しては、一意性を示せない。（ヒルベルト空間上の共役作用素に対しては、リースの表現定理で共役作用素の一意性を示せる）
この内積空間での一意性を示すための証明は以下の通り。
共役作用素 B の他に、
を満たすような写像 C が存在したとすると、
従って、共役作用素 B はただ１つのみ存在することが分かる。
- （証明略）(a) における、共役作用素が有界線形作用素であることのみ示す。
- (a) の証明
- まず、共役作用素 
が、線形作用素であることを示す。
有界線形作用素の共役作用素 
が存在するならば、
共役作用素の定義 
より、
任意の 
と任意の係数 
に対して、
となるので、
の関係より、共役作用素 は、線形作用素であることが分かる。
- 次に、共役作用素 が、有界であることを示す。
とおけば、
従って、共役作用素 は、有界線形作用素であり、
の関係が成り立つことが分かる。
☆ 共役作用素の行列表現（表現行列）
◎ 自己共役作用素（エルミート作用素）
（例）自己共役作用素の例（直交射影）
ヒルベルト空間 H からその部分空間 M⊂H への直交射影
は、
先の定理（ヒルベルト空間の閉部分空間への直交射影の線形性・冪等性・自己共役性）における自己共役性より、
の関係を満たすので、自己共役作用素である。【参考】
■ 凸最適化問題への応用
先に見てきた、ヒルベルト空間における射影定理は、無限次元の空間における幾何学的性質を与えてくれた。この射影定理とこれから導入される幾何学的性質は、凸最適化問題にも応用出来る。
ここでは、一般化された議論を行うために、「有限次元であるユークリッド空間での凸最適化問題」ではなく、「無限次元であるヒルベルト空間での凸最適化問題」を考えた上で、
以下のようなトピックを取り上げる。
- 「凸最適化問題が、変分不等式問題に帰着できること」
- 「変分不等式問題は、非線形写像の不動点を求める問題に帰着できること」
- 「凸関数がいくつかの条件を満たすとき、不動点の逐次近似アルゴリズムを用いて、
凸最適化問題の解がいくらでも精度良く近似出来ること」
そのための前段階として、まず、無限次元であるヒルベルト空間における凸集合や凸関数に関連する性質が、有限次元であるユークリッド空間と同様に成り立つのかを見ていく。
◎ ヒルベルト空間における弱点列コンパクト性と凸集合
先に、ヒルベルト空間における弱収束と強収束の違いを見てきたが、ヒルベルト空間の弱収束点列の弱極限と凸集合との非自明な関係性を見ていく。
- （証明略）step 1：部分列のある実数への収束性の証明のみ記載
- step 1：部分列のある実数への収束性の証明
ヒルベルト空間 H の有界な点列
に対しては、その有界性より、
の関係が成り立つ。
このとき、有界な点列 との内積の値からなる点列 
もまた、有界な実数列となるので、（ 
）
ここで、ハイネ・ボネルの被覆定理より、点列コンパクトなので、
有界な点列
に、少なくとも１つの部分列 
とある 
が存在して、
の関係が成り立つ。
同様の手続きで、部分列 の中に、さらなる部分列 
とある 
が存在して、
の関係が成り立つ。
同様の議論を繰り返すことにより、部分列
に対して、ある 
が存在して、
の関係が成り立つことが分かる。
- step 2：ヒルベルト空間の部分空間となる線形空間の存在性と、その空間上の有界線形作用素の証明
- step 3：ヒルベルト空間の部分空間となる線形空間が閉部分集合になることの証明
- step 4：部分列がヒルベルト空間の１点に収束することの証明
- step 1：部分列のある実数への収束性の証明
（証明略）
【参考】
◎ ヒルベルト空間における凸関数と基本性質
【Memo】
位相空間における下半連続性の定義との違いは？
- 【参考】
- （例）凸関数の例（自己共役作用素を用いて定義された関数）
ヒルベルト空間 H 上に定義された自己共役作用素 A:H→H とヒルベルト空間中のベクトル
を用いた関数
を定義する。
このとき、この関数
が凸関数となることと、
任意の
に対して、
が成り立つことが等価であることを示す。
任意の
に対して、
となるので、f:H→R が凸関数であれば、
従って、以下のような関係が成り立つ。
◎ ヒルベルト空間における凸関数と最小値の存在性
ヒルベルト空間における凸集合と凸関数は、以下の定理で示すように、（有限次元のユークリッド空間のときと同様にして）エピグラフという概念によって、関連付けることが可能である。
- （証明略）
- (a) の証明
図より、エピグラフが凸集合であることと、元の関数 f が凸関数であることが同値なことは自明。
又、エピグラフは閉集合であるととと、元の関数 f が下半連続であることが同値なことは自明。
- （証明）
関数 f は下半連続な真凸関数なので、先の定理（エピグラフとその性質）より、点列 
に対して、
ここで、内積部分の項は、
の条件より、
となる。
従って、この内積からなる点列 
は、有界であり、
下極限の定義より、
> 記載中...
- （証明略）２次元空間においては、図より自明
◎ ヒルベルト空間における凸関数の微分の単調性
- （証明）
- (a) ⇒ (b) の証明
ガトー微分の定義式
は、α∈R に関しての単調減少関数となっているので（計算略）、
任意の ∀λ∈R に対して、
の関係が成り立つ。
更に、
の関係より、
この式は、任意の 
に対して成り立っているので、
ヒルベルト空間中の任意の２点 
に対しては、
が成り立つことが分かる。
この２つの式の両辺を足し合わせると、定理の (b) の単調写像の条件
が導かれる。
- (b) ⇒ (a) の証明
ヒルベルト空間上の任意の固定されたベクトル 
に対しての線形結合 
を、
ガトー微分関係な写像 f で写像した 
を写像先とする写像、
は、λ=0 or 1 で変数 λ に対して微分可能であり、その微分（導関数）は、
となる。
又、ガトー微分での導関数 f′ が定理 (b) の単調写像の条件
を満たすので、
任意の 
に対して、
となるので、この関数 ψ は凸関数であることが保証され（途中計算略）、
が関係が成り立つ。
従って、
となり、ガトー微分可能な写像 f は凸関数であることが分かる。
- 【参照】
- （証明）
- (a) の証明
任意の ∀t∈(0,1) とある２つのベクトル 
に対して、
の関係が成り立つので、この距離関数 
は、凸関数である。
更に任意の 
に対して、
となるので、この距離関数 は、真凸関数となる。
- (b) の２乗距離関数 
の凸性証明
任意の ∀t∈(0,1) とある２つのベクトル に対して、
の関係が成り立つので、この２乗距離関数 は、凸関数である。
- (b) の２乗距離関数 のフレッシェ微分可能性の証明
任意の 
に対して、２乗距離関数の変化量は、
ここで、直交射影 
の定義より、この式から以下の２つの不等式が成り立つ。
従って、
更に、直交射影 の非拡大性より、
従って、先の不等式
で 
とすると、
- 【参照】
◎ 凸最適化問題と変分不等式問題と不動点問題
以下の定理は、「凸最適化問題」 と 「変分不等式問題」 と 「不動点問題」 とを結びつける定理であり、特に重要な定理となってる。
※ ヒルベルト空間における凸射影、直交射影の概念を使っていることに注目
- （証明）
- (a) ⇒ (b) の証明
ならば、
の間の点 
に対して、
が成り立つ。この式を変形して 
とすると、
- (b) ⇒ (a) の証明
ガトー微分可能な真凸関数 f の凸性より、
変形して、 とすると、
- (b) ⇔ (c) の証明
簡単な式変形となってる。
- (c) ⇔ (d) の証明
凸射影定理にある「凸射影の幾何学特徴付け」の関係
より
(c) の条件と (d) の条件を比較すると、
で対応しているので、(c) ⇔ (d) が成り立つ。
◎ ヒルベルト空間における射影勾配法
ここで、以下の定理で示すように、
特別な単調作用素 
に対しては、非線形である直交射影の合成写像 
における μ の設定を工夫することにより、この非線形である直交射影の合成写像 
を縮小写像や非拡大写像にすることが出来る。(＝非線形である直交射影の合成写像の非拡大性）
このことと、先の定理にあった、
「凸最適化問題 」⇔ 「変分不等式問題」⇔ 「（非線形である直交射影の合成写像に対する）不動点問題」の結論を組み合わせると、
種々の不動点定理（例えば、縮小写像の不動点定理など）から、変分不等式問題や不動点に関しての逐次近似アルゴリズム（例えば、射影勾配法など）を構築出来ることが分かる。
- （証明）
- (a) の証明
直交射影の合成写像（＝非線形写像）
の拡大性に関する式は、
となる。
従って、非線形な直交射影の合成写像 は、縮小写像になっていることが分かる。
- (b) の証明
定理にも示しているように、
非線形な直交射影の合成写像 が、縮小写像になるので、
縮小写像の不動点定理より、唯一の不動点 
に強収束する点列 
が存在する。
【Memo】凸最適化問題に対する関数解析（主にヒルベルト空間と凸射影、縮小写像の不動点定理）の適用
１．ヒルベルト空間における凸射影（直交射影）の非拡大性 → 縮小写像の不動点定理 → 不動点の逐次近似アルゴリズムの議論が可能になる。
２．凸最適化問題 → ヒルベルト空間における凸射影（直交射影）と単調写像やガトー微分の合成写像（非線形写像になる）に対する不動点問題に置き換え→この非線形写像の非拡大性 → 種々の不動点定理（縮小写像の不動点定理など） → 不動点の逐次近似アルゴリズムの議論（射影勾配法など）が可能になる。
- 【参照】
◎ 射影勾配法の一般化
先に見たように、凸最適化問題の古典的なアルゴリズム（射影勾配法）を、関数解析の視点（ヒルベルト空間、凸射影、直交射影、非拡大写像、縮小写像の不動点定理など）や不動点理論の視点から捉え直すことにより、凸最適化問題の古典的なアルゴリズム（射影勾配法）の非自明な一般化が可能となる。
☆ Mann の不動点近似定理と射影勾配法の弱収束定理
- （証明略）
以下の定理（Mann の不動点近似定理）は、非拡大写像の逐次近似を可能にする重要なアルゴリズムになっている。
- （証明略）
以下の定理（射影勾配法の弱収束定理）は、この定理（Mann の不動点近似定理）を凸最適化問題に適用することにより得られる定理である。
- （証明略）
☆ 射影 Landweber 法
射影 Landweber 法は、逐次近似アルゴリズムの１つであるが、射影勾配法の特別なケースでの一例となっている。
- （証明）
有界線形作用素 A の共役作用素 
を用いて、関数 Φ を表現し直すことを考える。
ここで、
従って、
ここで、先の例題（凸関数の例：自己共役作用素を用いて定義された関数）でみたように、
に対して、
関数 f:H→R が凸関数となることと、
任意の 
に対して、
が成り立つことが等価であるので、
今の 
の関係より、この関数 Φ は凸関数であることが分かる。
更に、この関数 Φ のフレッシェ微分（ガトー微分でもある）は、
となるので（計算略）、
となり、フレッシェ微分（ガトー微分でもある）
は非拡大写像であることが分かる。
そして、この結論（ は非拡大写像）に対して、射影勾配法を適用することが出来て、このアルゴリズム（射影 Landweber 法）が導かれる。
- 【参考】
☆ 並列射影法
並列射影法もまた、逐次近似アルゴリズムの１つであるが、射影勾配法の特別なケースでの一例となっている。
- （証明）
先の定理（ヒルベルト空間における閉凸集合への２乗距離関数の真凸性とフレッシェ微分）より、
閉凸集合への２乗距離関数として定義した Φ に対しては、フレッシェ微分可能となる。
従って、
のフレッシェ導関数が存在し、
ここで、
は非拡大写像なので、
従って、写像 
は非拡大写像となり、
である も非拡大写像となる。
従って、この結論（ は非拡大写像）に対して、射影勾配法を適用することが出来て、このアルゴリズム（並列射影法）が導かれる。
☆ ハイブリッド最急降下法
先に述べたように、射影勾配法によって逐次近似を行う点列を生成するためには、
や 
の非拡大写像の関係式より、閉凸集合への凸射影 
の計算が必要となる。
従って、この凸射影の計算が困難な場合には、射影勾配法では逐次近似を行えないという欠点がある。
しかしながら、凸射影の不動点全体からなる集合 
と、非拡大写像の不動点全体からなる集合 
とが等しく、これらの不動点全体の集合が、ヒルベルト空間の閉凸部分集合 C⊂H となるような場合、
即ち、
となるような場合においては、非拡大写像 T の計算を簡単に行うことが出来るケースが存在する。
このような場合において、威力を発揮する逐次近似アルゴリズムが、ハイブリッド最急降下法である。
この逐次近似アルゴリズムは、凸射影 の代わりに、一般の非拡大写像 T を逐次近似を行う点列の生成に利用できるようにしており、
「非拡大写像 T の不動点全体の集合 Fix(T) 上での凸関数 f の最小化 
を実現する。」
このことを示したのが、以下のハイブリッド最急降下法の収束定理である。
☆ アンカー法
ハイブリッド最急降下法の特別な場合として、アンカー法が導かれる。
具体的には、ハイブリッド最急降下法における凸関数 f として、
を選ぶと、先のハイブリッド最急降下法における近似点列の更新式
の関係より、
の更新式が導出される。
そして、この式は、アンカー法の逐次近似アルゴリズムとなっている。
■ 参考文献
- 作者: 山田功
- 出版社/メーカー: 数理工学社
- 発売日: 2009/05/01
- メディア: 単行本
- 購入: 1人 クリック: 7回
- この商品を含むブログ (2件) を見る
- 作者: 黒田成俊
- 出版社/メーカー: 共立出版
- 発売日: 1980/11/01
- メディア: 単行本
- 購入: 1人 クリック: 15回
- この商品を含むブログ (7件) を見る
新版 応用のための関数解析―その考え方と技法 (SGC BOOKS)
- 作者: 吉田善章
- 出版社/メーカー: サイエンス社
- 発売日: 2006/10/01
- メディア: 単行本
- 購入: 1人 クリック: 2回
- この商品を含むブログを見る
