線形代数学

線形代数学に関してのマイノートです。今後も随時追加予定です。
あまり厳密でないので数学科or出身者の方から見たら天下り的説明に見えるかと思いますがご了承ください。

項目 [Contents]

1. 概要、全体 MAP [Overview]
2. ベクトル [vector]
   1. ベクトル空間 [vector space]
      1. ベクトル空間とベクトルの性質
         1. 張る（生成する）
         2. 線形独立（一次独立）と線形従属（一次従属）
            1. 線形独立（１次独立）[linearly independent] と線形従属（１次従属）[linearly dependent] のイメージ
      2. 基底ベクトル [basis vector]
      3. ベクトルの次元
3. 行列 [Matrix]
   1. ガウスの消去法 [Gaussian elimination]
   2. 行列式 [determinant]
   3. 行列式の性質
   4. ガウスの消去法を利用した行列式の計算
   5. 余因子展開 [cofactor expansion]
   6. 行列式の積
   7. 置換による行列式の表現
      1. 置換の符号
      2. 置換による行列式の定義
   8. 逆行列 [inverse matrix]
      1. 逆行列の公式
      2. 逆行列の公式を用いての逆行列の算出
      3. ガウスの消去法を用いての逆行列の算出
   9. 行列のランク（階級）[rank]
      1. 行列のランクの意味
         1. 小行列式によるランクの定義
      2. 連立１次方程式と行列のランクの関係
   10. 転置行列 [transposed matrix]、対称行列 [symmetric matrix]
   11. 複素行列と複素共役、共役転置行列（随伴行列） [adjugate matrix]
4. 線形写像 [linear mapping]
   1. 線形変換 [linear transformation]
      1. 線形変換の幾何学的イメージ
      2. アファイン変換 [affine transformation]
      3. 線形変換の逆変換
   2. 線形写像 [linear mapping]
      1. 線形写像の核 [kernel] と像 [image]
      2. 商空間 [quotient space]
      3. 線形代数学の基本定理
         （線形写像の商空間と像の関係＋カーネルと像の次元の関係、準同型定理の特殊なケース）
      4. 連立１次方程式への線形代数学の基本定理の応用
5. 固有値 [eigenvalue]、固有ベクトル [eigenvector]
   1. 固有方程式
   2. 特性方程式
6. 行列の対角化 [diagonalization]
   1. 対角化可能な条件
   2. なぜ対角化するのか？
      1. ２次形式の標準化への応用
   3. 直行行列 [orthogonal matrix] と実対称行列 [symmetric matrix]
   4. エルミート行列 [Hermitian matrix] とユニタリー行列 [Unitary matrix] の対角化
      1. エルミート行列 [Hermitian matrix]
      2. ユニタリー行列 [Unitary matrix]
      3. エルミート行列のユニタリー行列での対角化
7. ジョルダン標準形 [Jordan normal form]
   1. ２×２行列でのジョルダン標準形
   2. ジョルダン標準形の微分方程式への応用
8. ベクトル解析 [vector calculus]
   1. 内積 [inner product]
   2. 外積 [cross product]
   3. 勾配 [gradient] : grad f = ∇ f
   4. 発散 [divergence] : div A = ∇・A
   5. 回転 [rotation] : rot A = ∇ × A

9. 参考文献

10. 追記予定項目

    • グラム・シュミットの正規直交化法 [Gram–Schmidt orthonormalization]
    • 行列の QR 分解 [QR decomposition]
    • 行列の特異値分解 [SVD : single value decomposition]
    • ３×３行列でのジョルダン標準形

概要 [Overview]

ベクトル [vector]

ベクトル空間 [vector space]

• （例）
  １階の線形微分方程式
  
  において、方程式の解（ベクトル）
  
  のすべてからなる集合 V はベクトル空間であることを示す。
  

  １階の線形微分方程式の解 に対して、公理 (1),(2),(5),(6) は自明に成り立つ。
  また、【定理１】より (7),(8) も成り立つ。
  公理 (3) は、 に対して、
  公理 (4) は、 とすると、
  
  つまり、 は、この微分方程式の解であり、集合 V に含まれるので成り立つ。（公理(4)を満たす）
  よって、１階の線形微分方程式の解全体の集合はベクトル空間となる！
  

ベクトル空間とベクトルの性質

張る（生成する）

線形独立（一次独立）と線形従属（一次従属）

線形独立（１次独立）[linearly independent] と線形従属（１次従属）[linearly dependent] のイメージ

基底ベクトル [basis vector]

ベクトルの次元

行列 [Matrix]

ガウスの消去法 [Gaussian elimination]

行列式 [determinant]

行列式の性質

ガウスの消去法を利用した行列式の計算

余因子展開 [cofactor expansion]

行列式の積

置換による行列式の表現

置換の符号

置換による行列式の定義

逆行列 [inverse matrix]

逆行列の公式

逆行列の公式を用いての逆行列の算出

ガウスの消去法を用いての逆行列の算出

行列のランク（階級）[rank]

行列のランクの意味

小行列式によるランクの定義

記載中...

連立１次方程式と行列のランクの関係

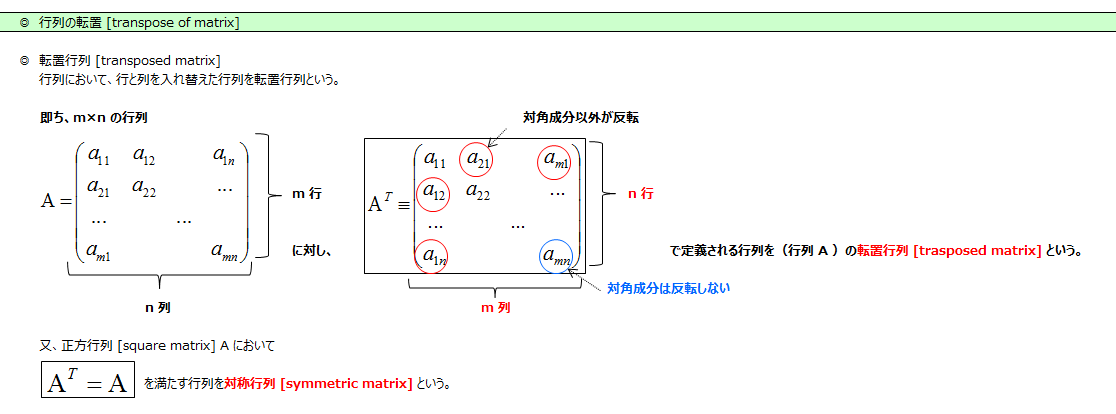
転置行列 [transposed matrix]、対称行列 [symmetric matrix]

複素行列と複素共役、共役転置行列（随伴行列） [adjugate matrix]

線形写像 [linear mapping]

線形変換 [linear transformation]

線形変換の幾何学的イメージ

アファイン変換 [affine transformation]

線形変換の逆変換

線形写像 [linear mapping]

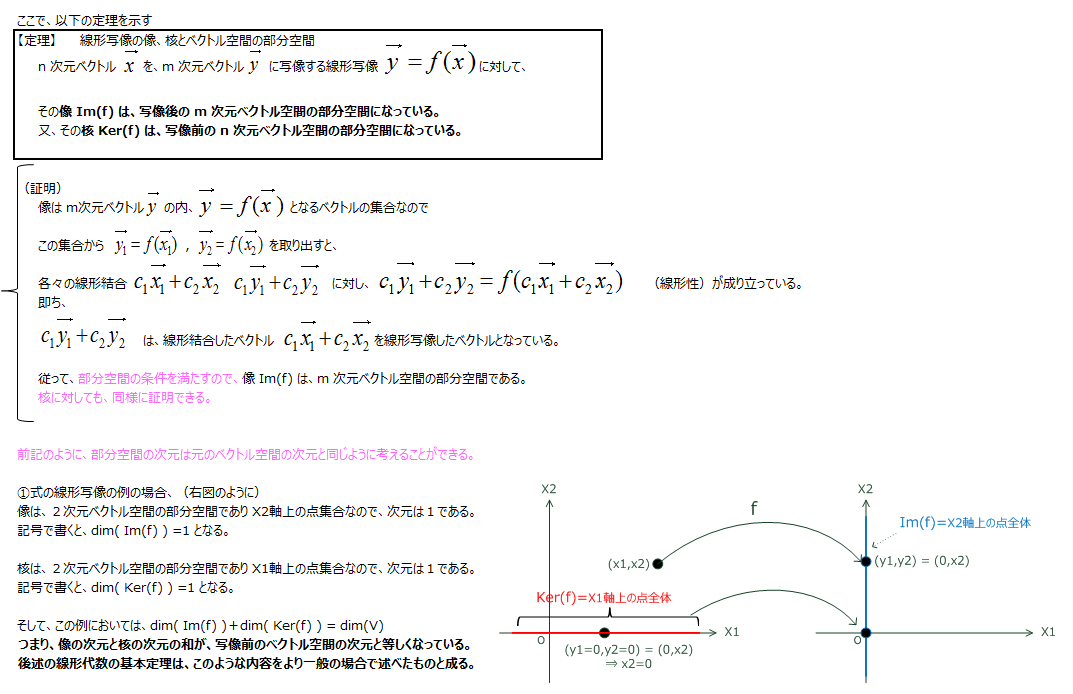
線形写像の核 [kernel] と像 [image]

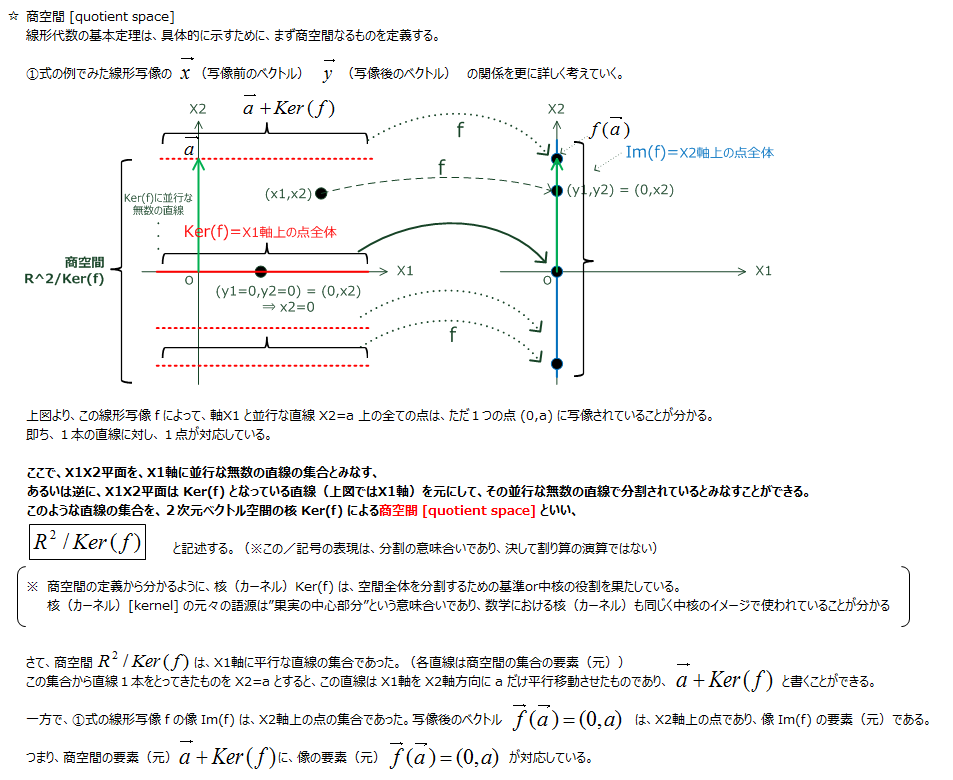
商空間 [quotient space]

線形代数学の基本定理（線形写像の商空間と像の関係＋カーネルと像の次元の関係、準同型定理の特殊なケース）

連立１次方程式への線形代数学の基本定理の応用

固有値 [eigenvalue]、固有ベクトル [eigenvector]

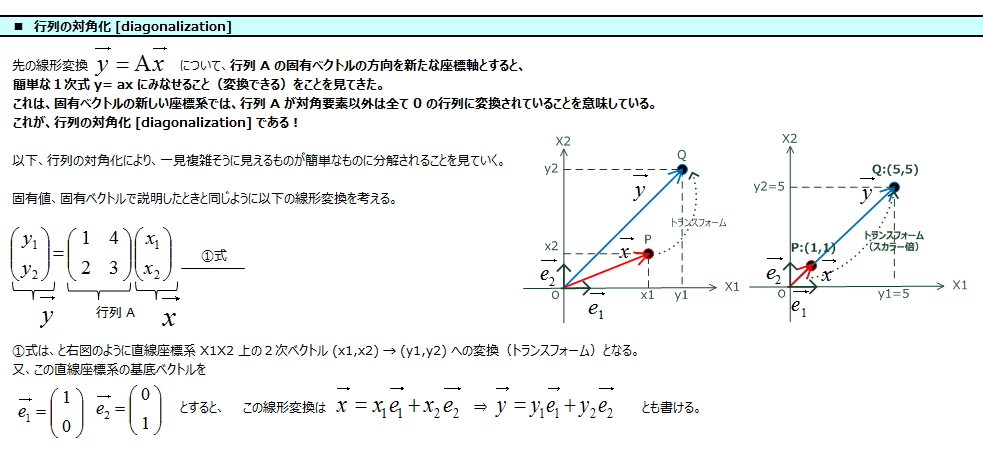
行列の対角化 [diagonalization]

対角化可能な条件

なぜ対角化するのか？

２次形式の標準化への応用

直行行列 [orthogonal matrix] と実対称行列 [symmetric matrix]

エルミート行列 [Hermitian matrix] とユニタリー行列 [Unitary matrix] の対角化

エルミート行列 [Hermitian matrix]

ユニタリー行列 [Unitary matrix]

エルミート行列のユニタリー行列での対角化

ジョルダン標準形 [Jordan normal form]

２×２行列でのジョルダン標準形

ジョルダン標準形の微分方程式への応用

ベクトル解析 [vector calculus]

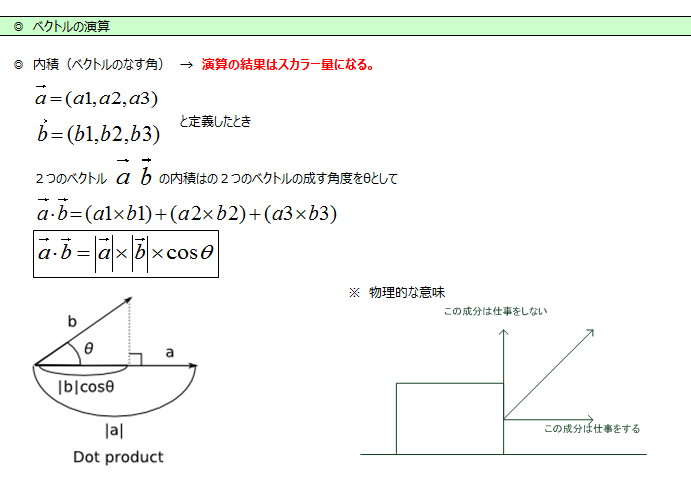
内積 [inner product]

外積 [cross product]

勾配 [gradient] : grad f = ∇ f

発散 [divergence] : div A = ∇・A

回転 [rotation] : rot A = ∇ × A

参考文献

キーポイント線形代数 (理工系数学のキーポイント 2)

詳解演習 線形代数 (詳解演習ライブラリ)

情報数理の基礎と応用 (ライブラリ情報学コア・テキスト)