統計力学 [statistical mechanics]

統計力学に関してのマイノートです。今後も随時追加予定です。

項目 [Contents]

概要 [Overview]
系の微視的状態 [microscopic state] と巨視的状態
1. 相空間 [phase space]
2. ある系の物理量の平均値
等重率の原理とミクロカノニカルアンサンブル
カノニカルアンサンブル [canonical ensemble]
1. 分配関数 [partition function]
2. 例題
グランドカロニカルアンサンブル [grand canonical ensemble]
古典理想気体への適用
理想フェルミ気体、ボーズ気体の熱力学量
1. １粒子のエネルギー状態密度
  1. （例題）古典理想気体でのエネルギー状態密度の使い方
2. 理想フェルミ気体 1.（例題）金属中の電子
3. ベルヌーイの式の証明
4. 理想フェルミ気体とフェルミ縮退
  1. 縮退した理想フェルミ気体
    1. （例題）金属中の伝導電子
    2. （例題）金属強磁性体
5. 理想ボース気体とボース凝縮
  1. （例題）ヘリウム 4 He
6. ボーズ・アインシュタイン凝縮 [BEC : Bose-Einstein condensation]
1. （例題）調和振動子系
2. （例題）立方体に閉じ込められた電磁波
内部自由度
非理想気体
1. 非理想気体の相互作用する中性分子気体の熱力学量
2. ビリアル展開
3. ファンデルワールス方程式
4. ギブスの自由エネルギー
5. ヘルムホルツの自由エネルギー
6. ビリアル係数の別の導出
7. ジュールトムソン効果（リンデの液化装置の原理）

系の微視的状態 [microscopic state] と巨視的状態量

今、上図のような系があったとする。
このとき、この系の 微視的状態 が定まるとは、この系の全ての粒子についての力学変数（位置、運動量）が定まった状態、つまり、それぞれの粒子に対しての運動方程式が定まった状態である。
一方、この系の 巨視的状態 が定まるとは、この系全体を特徴付ける量、即ち、系全体の圧力、温度などが定まった状態である。
実用上役に立つのは系の巨視的状態量（情報）である。
ここでの目的は、熱平衡状態 [thermodynamic equilibrium] にある系の微視的状態から、巨視的状態量を導くことである。そして、後述するように 系の巨視的状態量は、系の微視的状態量の平均値から求まる！ のである。

しかしまず、微視的状態の意味を詳しく検討するため、相空間 [phase space] の概念を導入する。

相空間 [phase space]

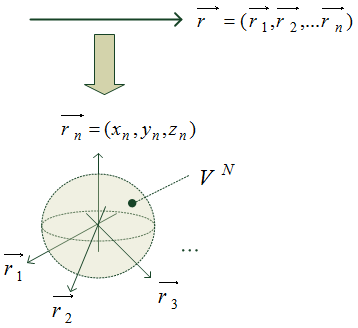
今、例えば n 個の粒子よりなる系を考える。
このとき、それぞれの粒子についての
位置 : 運動量 : を定めれば、（つまり、系の微視的状態を定めれば）
Hamiltominan

が求まり、
それぞれの粒子についての運動方程式

が定まる。

ここで、それぞれの粒子について定めた、位置 : 運動量 :

を変数とする 6N 次元空間を 相空間 という。

すると、系の微視的状態を定めるとは、相空間上の一点を指定することと同値であることが分かる。
また、このとき系のそれぞれの粒子は、相空間上のエネルギー E (=H) が一定の軌道（面）を先の運動方程式 (1-1) 式に従って運動する。

ある系の物理量の平均値

話を元に戻そう。
今、我々の目的は、熱平衡状態にある系の微視的状態から巨視的状態量を導くことであった。そして、巨視的状態量は、微視的状態量の平均から求まるのであった。

今、例として N 個の粒子よりなる系を考える。
このとき、系の粒子は、位置と運動量の相空間上の等エネルギー面を、式 (1-2) 式に従って、運動する。

今、ある１つの微視的状態量をとすると、

これに対応する巨視的状態量は A の平均値＜ A ＞となり、

とかける。（左辺：A の平均値で観測される巨視的状態量、右辺：時間に対する平均）

あるいは、A の相空間の（等エネルギー面での）確率分布 P が与えられる時、

となる。（これを アンサンブル平均 という。）

※量子系で離散的な時は、

となる。

これらの式より、＜A＞を求めるには、位置と運動量を求めなくてはならない。
つまり、系の全ての粒子についての運動方程式 (1-1) 式を解かなければならず、粒子数 N が大きい時、これは実際上不可能である。
しかし 「等重率の原理 [principle of equal a priori probabilities]」 の仮定の元では、（ある物理量 A の確率分布 P が求まり）(1-3) 式は計算可能となる！

等重率の原理とミクロカノニカルアンサンブル

等重率の原理 [principle of equal a priori probabilities]（仮定）

N 個の粒子よりなる熱平衡状態にある孤立系を考える。
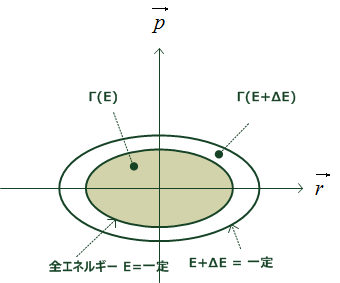
E ~ E + ΔE の間の相空間の体積を Γ(E, ΔE) とする。

このとき、” Γ(E, ΔE) 内のどの点も同じ確率 P で実現される”
言い換えれば、”可能な微視的状態は、全て同じ状態で実現される”
と仮定する。この仮定が、等重率の原理 である。
よって、Γ(E, ΔE) 内の微視的状態の数を W(E) とすると、

とかける。

ミクロカノニカルアンサンブル [microcanonical ensemble]

では、この一定の確率 P を求めてみる。
今、可能な微視的状態（Γ(E, ΔE) 内の点）の数を W(E) とすると、等重率の原理より、これらは全て同じ確率で起こるので、当然

となる。（例えば、W(E)=2 のとき、1/2 と 1/2、W(E)=3 のとき、1/3 と 1/3 と 1/3）

可能な微視的状態の確率分布が (2-2) 式 P=1/W(E)（一定）となるようなものを、ミクロカノニカル分布 [microcanonical distribution] という。
つまり、ミクロカノニカルアンサンブル とは、(1-3) 式の確率分布が

で与えられる集団である。

さて、これで (1-3) 式の確率分布が求まったので、(1-3) 式は計算可能となり、任意の微視的状態量 A の平均値＜A＞（巨視的状態量）は計算可能となった。（※この手法による方針を、方針①とする）

しかし、系のエントロピー S が、

（k_B : ボルツマン定数）

となるとすれば、このエントロピー S より、熱力学関係式を使って、他の巨視的状態量を (2-5),(2-6),(2-7) 式より導くことも出来る。（※この手法による方針を、方針②とする）

※エントロピー S と他の巨視的状態量の関係

T : 温度
p : 圧力
V : 体積
μ : 化学ポテンシャル
N : 物質量

どちらの方法でも、まず W(E) を求める必要がある。
W(E) は、(2-1) 式

より、Γ(E,ΔE) を求めれば良い。

更に、Γ(E,ΔE) は

より、Γ(E) を求めれば良い。

例題

（例題１）孤立系での巨視的状態量

熱平衡状態にある質量 m の N 個の粒子よりなる、体積 V の孤立系の巨視的状態量を求める。

まず、W(E) を求める。（これが分かれば、P_mc = 1/(W(E)) あるいは S=k_B log( W(E) ) が分かる）
そのためには、

より、Γ(E,ΔE) を求めれば良く、
更に、Γ(E,ΔE) は

より、Γ(E) が求めれば良い。

この系の Hamiltonian は、

（3N 個）

Γ(E) は、

①式より、

ここで、積分範囲は、

　とおくと、

つまり、 R は、半径の球の内部であり、
この積分は、3N 次元空間の、半径の球の体積である。
そして、この体積をとかくことにする。

よって、F(E) は

となる。

次に、この式の項

を求めるため、以下のようなトリックを使う。

　とすると、

一方、

　とおくと、

ここで、

なので、

　とおくと、

　Γ：ガンマ関数

ガンマ関数の関係式より、

よって、③式より、

よって、n 次元空間の半径 r の体積 Vn は、

よって、②式は、

　（最後の式変形は、ガンマ関数の関係式より）

よって、Γ(E+ΔE) は、

よって、目的である W(E) は、

N! : N 個の粒子が区別できないため

この W(E) を使って、微視的状態の実現確率 Pcm = 1/W(E) を求め、(1-3) 式に代入し、ある物理量 A の巨視的状態量＜A＞を求める方法（方針①）と、エントロピー S = k_B log W(E) を求め、熱力学の関係式 (2-5), (2-6), (2-7) から巨視的状態量を求める方法があるが（方針②）、ここでは後述の方法（方針②）で巨視的状態量を求めることにする。

エントロピー S は、⑤式より、

ここで、

　となることと、

String の公式

　より

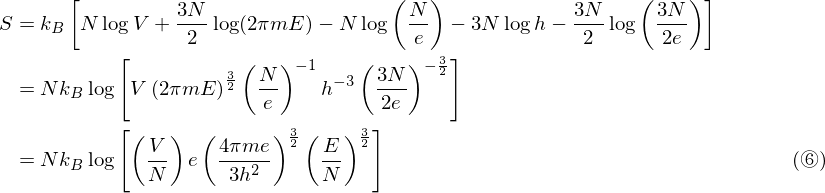
エントロピー S が求まったので、他の巨視的状態量を、以下の熱力学関係式より求める。

T : 温度
p : 圧力
V : 体積
μ : 化学ポテンシャル
N : 物質量

まず、エネルギー E は、

の関係より、

よって、エネルギー E は、

圧力 p は、

の関係より、

よって、圧力 p は、

化学ポテンシャル μ は、

の関係より、

　の関係を代入すると、
化学ポテンシャル μ は、

ヘルムホルツの自由エネルギー F は、

　の関係を代入すると、
Helmholz の自由エネルギー F は、

（例題２）２準位系での巨視的状態量

N 個の粒子よりなる孤立系があり、それぞれの粒子のエネルギーは、+ ε0 か -ε0 であったとする。
このとき、この系の巨視的状態量をミクロカノニカルアンサンブルの考えから求める。

記載中...

カノニカルアンサンブル [canonical ensemble]

前節で、ミクロカノニカル集合を用いて、微視的状態量から巨視的状態量を導いた。
全ての系は、そのサイズを非常に大きくとると、原理的には孤立系となるので、ミクロカノニカル集合を用いて全ての巨視的状態量が計算可能であると思われる。
しかし、ミクロカノニカル集合を用いた計算は、先の例で見たように非常に大変である。

ここでは、より実用的な方法として、カノニカル集合を考える。

今、上図のような熱平衡状態にある系を考える。
熱平衡状態にあるので、reserve system と sub system の温度は同じである。

reserve system と sub system の間では、エネルギーは出入り可能であるとする。つまり、sub system 内のエネルギー Es は一定でないので等重率の原理は成り立たない。
又、全系 [toatl system] は孤立系であるとする。

つまり、

が成り立つ。

今、考えることは、sub system が、ある特定の微視的状態 i になる確率 Pi である。

sub system のある特定の微視的状態 i である数は、当然１個
つまり、　である。

一方、reserve system の微視的状態の数は、(2-1) 式より、

　とかける。

よって、sub system が、ある特定の微視的状態 i になる確率 Pi は、

とかける。（分母 Wt(Et) は全系の微視的状態の数）

ここで、(2-2) 式の　　の項は、エントロピーの式と Tayer 展開を使用して、

ここで、

　　の関係より

(2-2) 式に代入すると、

ここで、確率の条件

　　より、

よって、sub system がある特定の微視的状態 i となる確率は、

で与えられる。

sub system の微視的状態の実現確率が (2-3) 式で与えられるものをカロニカル集団という。

つまり、カロニカル集団とは、(1-3) 式の確率分布が、

で与えられる集団である。

左辺：n 番目の微視的状態の実現確率
分母：可能な全ての微視的状態の和（分配関数という）

※古典力学系では、連続なので (2-4) 式の分母の ∑ は、∫ になる。

分配関数 [partition function]

先のカロニカル集団における実現確率 (2-4) 式の分母の項

を分配関数というが、

巨視的状態量 (1-3) 式は、まずこの分配関数 Z を求めることが重要となる。
即ち、以下の２つの巨視的状態量を求める手法双方で、まず分配関数 Z を求める必要がある。

（方針１）
分配関数 Z が求まれば、カロニカル集団の実現確率 (2-4) 式が求められ、これを使って、巨視的状態量 (1-3) 式が計算可能となる。

（方針２）
（ミクロカノニカル集団のときと同様にして）
ヘルムホルツの自由エネルギーが

（Z : 分配関数）となるとすれば、他の巨視的状態量は熱力学関係式より求まる。

※ ヘルムホルツの自由エネルギーと他の巨視的状態量の関係

F : ヘルムホルツの自由エネルギー
S : エントロピー
T : 温度
N : 物質量
p : 圧力
V : 体積

※ エントロピー S は、ヘルムホルツの自由エネルギー F を求め、

から求めてもよいが、カロニカル分布 (2-4) 式を直接使うと、

　　と書ける。（証明略）

例題

（例題１）古典理想気体での巨視的状態量

熱平衡状態にある体積 V で質量 m の N 個の粒子よりなる古典理想気体の巨視的状態量を求める。

まず、分配関数

　　を求める。

この系のハミルトニアンは、

（3N 個）

よって分配関数 Z は、

　（最後の式変形は、積分範囲がどれも同じなので）

　の関係式より [...] の中身の部分は、

よって、

この分配関数 Z を使って、カロニカルアンサンブルの確率分布
　を求め、アンサンブル平均 (1-3) 式より巨視的状態量を求める方法（方針①）と、
ヘルムホルツの自由エネルギーが F = - k_B T log Z で与えられるとして、他の巨視的状態量を熱力学関係式から求める方法（方針②）があるが、ここでは２つ目の方法でいく。